Day 24: Crossed Wires
Megathread guidelines
- Keep top level comments as only solutions, if you want to say something other than a solution put it in a new post. (replies to comments can be whatever)
- You can send code in code blocks by using three backticks, the code, and then three backticks or use something such as https://topaz.github.io/paste/ if you prefer sending it through a URL
FAQ
- What is this?: Here is a post with a large amount of details: https://programming.dev/post/6637268
- Where do I participate?: https://adventofcode.com/
- Is there a leaderboard for the community?: We have a programming.dev leaderboard with the info on how to join in this post: https://programming.dev/post/6631465


Haskell
Part 1 was trivial, just apply the operations and delay certain ones until you have all the inputs you need.
Code
For part 2 I tried symbolic solving to detect discrepancies but I wouldn’t achieve anything with it.
SymbolicEquation
My solution was to use the
dotEngine-function to translate the operations into a digraph in graphviz-style which I simply plotted and searched through using a python script.dotEngine
I took a loook at the initial graph which was a vertical line with a few exception which I figured would be the misordered wires. I did try some hardware-simulations in the far past to build bit-adders which helped me recognize patterns like carry calculation. First I replaced all occurences of
x__ XOR y__ -> wwithx__ XOR y__ -> xor__to recognize them more easily. The same withANDof xs and ys. Using the following script I would then use some Regex to search for the rules that corresponded to carry calculations or structures I knew. The script would break exactly four times and I would then figure out what to switch by hand through looking at the updated graphViz.Please excuse the bad coding style in the script, I had written it on the ipython-REPL.
python script
When solving such a swapped wire problem I would then use my haskell function to plot it out again and stare at it for a few minutes until I understood wich parts belonged where.
The last one looked like this
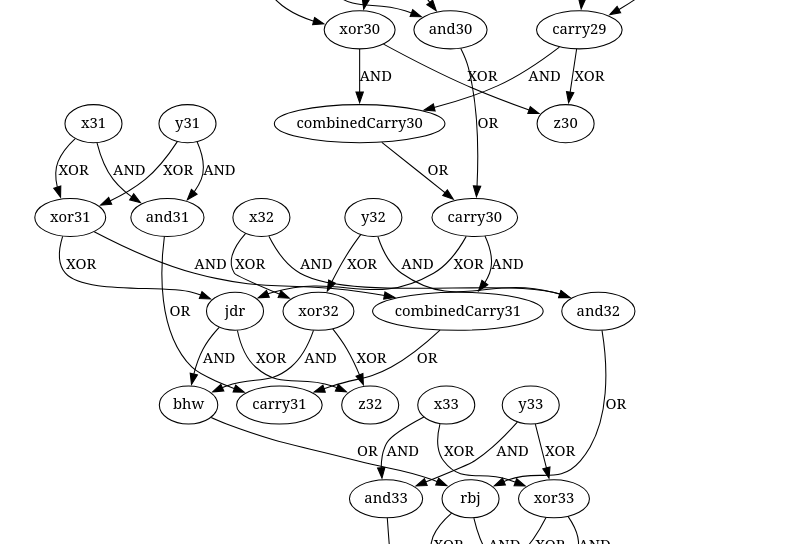
In this one I needed to switch
jdrandcarry31to make it work.